Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

A square tower stands upon a horizontal plane. From a point in this plane, from which three of its upper corners are visible, their angular elevations are respectively 45 dergrees, 60 degrees and 45 degrees. Show that the height of the tower is to the breadth of one of its sides as √6(√5+1) to 4.
please answer fast...all help appreciated :-D
Asked by reetatyagi8 | 31 May, 2015, 12:53: PM
answered-by-expert Expert Answer
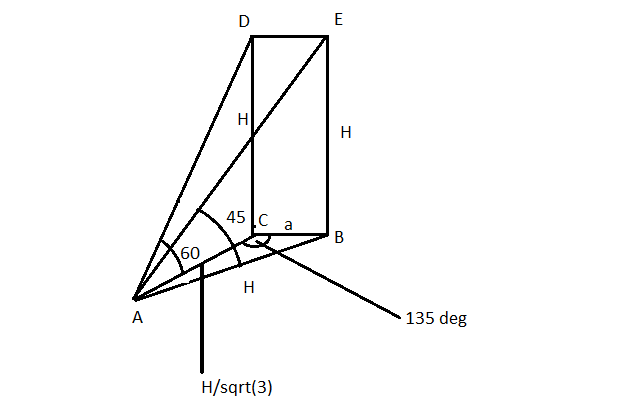
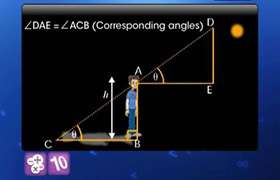
One face of the tower with two upper corners 'D' and 'E' is shown in the figure.
'D' makes 60o with a point 'A' in the plane. Hence, 
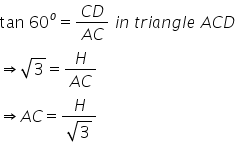
tan space 60 to the power of o equals fraction numerator C D over denominator A C end fraction space i n space t r i a n g l e space A C D rightwards double arrow square root of 3 equals fraction numerator H over denominator A C end fraction rightwards double arrow A C equals fraction numerator H over denominator square root of 3 end fraction
 
The corner 'E' makes an angle of 45o with point 'A' in the plane. Hence,
tan space 45 to the power of o equals fraction numerator E B over denominator B A end fraction space i n space t r i a n g l e space A B E rightwards double arrow 1 equals fraction numerator H over denominator A B end fraction rightwards double arrow A B equals H
 
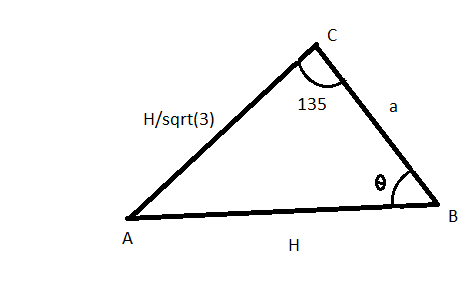
In triangle ABC, the angle ACB=135o (using symmetry, since the angle is same 45o with two upper corners)
Triangle ABC is redrawn below:
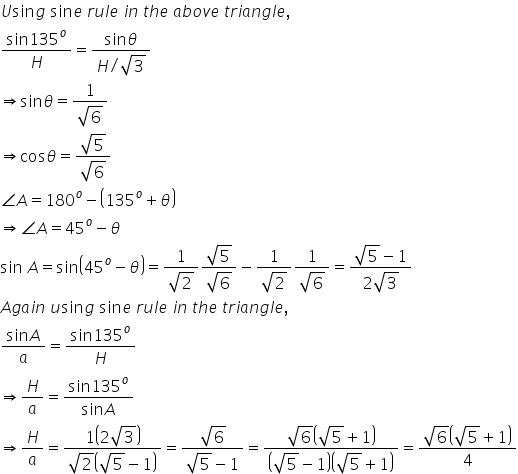
U sin g space sin e space r u l e space i n space t h e space a b o v e space t r i a n g l e comma space fraction numerator sin 135 to the power of o over denominator H end fraction equals fraction numerator sin theta over denominator H divided by square root of 3 end fraction rightwards double arrow sin theta equals fraction numerator 1 over denominator square root of 6 end fraction rightwards double arrow cos theta equals fraction numerator square root of 5 over denominator square root of 6 end fraction angle A equals 180 to the power of o minus open parentheses 135 to the power of o plus theta close parentheses rightwards double arrow angle A equals 45 to the power of o minus theta sin space A equals sin open parentheses 45 to the power of o minus theta close parentheses equals fraction numerator 1 over denominator square root of 2 end fraction fraction numerator square root of 5 over denominator square root of 6 end fraction minus fraction numerator 1 over denominator square root of 2 end fraction fraction numerator 1 over denominator square root of 6 end fraction equals fraction numerator square root of 5 minus 1 over denominator 2 square root of 3 end fraction A g a i n space u sin g space sin e space r u l e space i n space t h e space t r i a n g l e comma fraction numerator sin A over denominator a end fraction equals fraction numerator sin 135 to the power of o over denominator H end fraction rightwards double arrow H over a equals fraction numerator sin 135 to the power of o over denominator sin A end fraction rightwards double arrow H over a equals fraction numerator 1 open parentheses 2 square root of 3 close parentheses over denominator square root of 2 open parentheses square root of 5 minus 1 close parentheses end fraction equals fraction numerator square root of 6 over denominator square root of 5 minus 1 end fraction equals fraction numerator square root of 6 open parentheses square root of 5 plus 1 close parentheses over denominator open parentheses square root of 5 minus 1 close parentheses open parentheses square root of 5 plus 1 close parentheses end fraction equals fraction numerator square root of 6 open parentheses square root of 5 plus 1 close parentheses over denominator 4 end fraction
Answered by satyajit samal | 01 Jun, 2015, 11:59: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
Two pillars are standing on either side of a 80 m wide road. Height of one pillar is 20 m more than the height of the other pillar. From a point on the road between the pillars, the angle of elevation of the higher pillar is 60°, whereas that of the other pillar is 30°. Find the position of the point between the pillars and the height of each pillar. (Use √3 = 1-73)
Asked by swetalinasamantaray022 | 21 Mar, 2023, 04:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Two buildings face each other. The height of one building is greater than that of the other. The smaller building is 80 m high. The angles of depression of the top and the bottom of the smaller building from the top of the taller building are 45º and 60º respectively. Find the height of the taller building.
Asked by shanbhog.06 | 14 Apr, 2022, 11:26: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
On a warm and lazy Saturday, Rishi is watching a county maintenance crew mow the park across the street. He notices the mower takes 16 sec to pass through 60c of rotation from one end of the park to the other. If the corner of the park is 40 meter directly across the street from his house,  (i) How wide is the park?  (ii) How fast (in kmph) does the mower travel as it cuts the grass?
Asked by badakhsharda | 14 Apr, 2022, 08:57: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is √st.
Asked by naancysingh | 09 Apr, 2022, 07:07: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
a person standing on the bank of a river observes that the angle subtented by a tree on the opposite bank of 60 degree. when he retreates 20m from the bank he find the angle to be 30 degree . find the height of the tree and the bradth of the river
Asked by vy499292 | 23 Jan, 2022, 08:04: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
In triangle ABC, AD is perpendicular to BC, angles B and C are of measures 30 and 60 respectively, if AD=7m, then find the value og BC.
Asked by godboletanaya | 24 Dec, 2021, 11:08: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
cos theta +cos theta is equal to
Asked by nikunjgupta102021 | 12 Jul, 2021, 09:01: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If two crows are sitting at a height of 15 m and 10 m on different trees vertically opposite to each other. They view a vaddi (an estable) on the ground at a angle of depression 45°and 60° respectively. They start at the same time and fly at the same speed along the shortest path to pick up the vadai.Which bird will succeed in it.?
Asked by urzashu7818 | 15 Jan, 2021, 12:52: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
question
question image
Asked by arindeep.singh | 02 Oct, 2020, 12:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
question
question image
Asked by arindeep.singh | 02 Oct, 2020, 12:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×