CBSE Class 12-science Answered
A square loop of side 12 cm with its side parallel to x and y axis move with velocity of 8 cms^-1in
the positive x direction in an environment containing a magnetic field in this positive z direction.The
field is neither uniform in space nor constant in time.It has a grdient of 10^-3 Tcm^-1 along the negative x direction (i.e., it increases by 10^-3 Tcm^-1 along the negative x direction i.e.it increases
by 10^-3 Tper cm as one moves in the -ve x direction),and it is decreasing in time at the rate 10^-3
Ts^-1.Determine the direction and magnitude of the induced current in the loop if its resistance is 4.5
m ohm.
Asked by Balbir | 26 Jul, 2017, 09:03: PM
The following steps and pointers need to be followed for solving the query:
1) First, find the area of the loop as it is inside the field. A = 144 × 10-4 m2.
2) Consider the time variation of the field. It is 10-3 Ts-1 With this, we get the change of flux due to time variation as (dΦ/dt)t = εt = (B/t)A = 10-3 Ts-1 × 144 × 10-4.
3) Flux due to motion of loop in non-uniform field is (dΦ/dt)v = (B/t)Av = εv.
4) Add both the values of emf to get the total induced emf.
5) Find the induced current by I = ε/R.
6) Note that the direction of induced current will be such as to increase the current through +z direction.
Answered by Romal Bhansali | 28 Jul, 2017, 01:43: PM
Concept Videos
CBSE 12-science - Physics
Asked by azadtanbir682 | 14 Jun, 2023, 11:28: PM
CBSE 12-science - Physics
Asked by yadavabhishek66686668 | 24 Jan, 2023, 05:32: PM
CBSE 12-science - Physics
Asked by sahilposwal28 | 21 Aug, 2020, 02:20: PM
CBSE 12-science - Physics
Asked by abhitailor158 | 21 Apr, 2020, 10:07: AM
CBSE 12-science - Physics
Asked by alanpeter9611 | 01 Mar, 2019, 12:47: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 07 Jul, 2015, 11:18: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 07 Jul, 2015, 11:24: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 07 Jul, 2015, 11:36: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 07 Jul, 2015, 11:36: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM








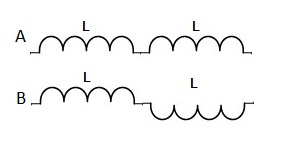 Suppose the two coils with inductance L are connected as shown in the diagram above. Calculate the total self inductance.
Suppose the two coils with inductance L are connected as shown in the diagram above. Calculate the total self inductance.