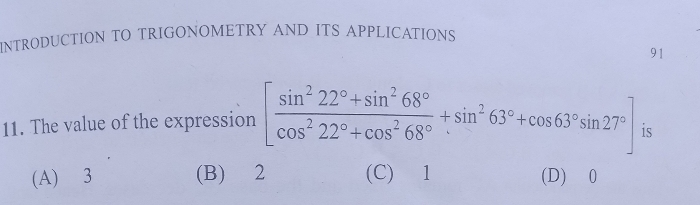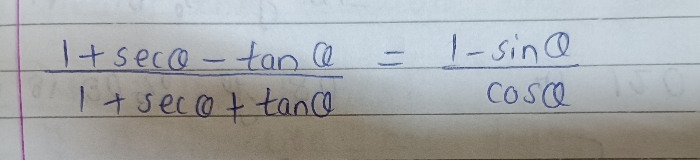Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

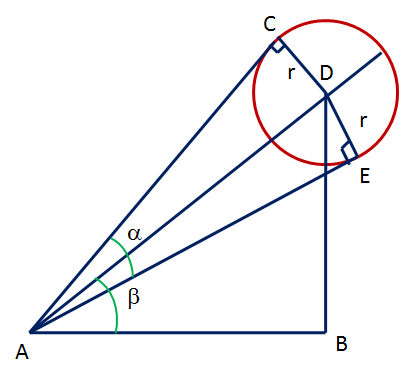
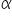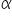A round ball of radius r subtends an angle alpha at  the eye  of the observer while the angle of elevation of its centre is beta.Prove that the height of the centre of the balloon is r sinbold italic beta bold space bold italic c bold italic o bold italic s bold italic e bold italic c bold space bold italic alpha bold divided by bold 2
Asked by afreensyed13 | 14 Feb, 2017, 07:57: AM
answered-by-expert Expert Answer
begin mathsize 16px style To space prove colon space height space equals DB equals straight r space sinβ space cosec straight alpha over 2 In space increment ACD space and space AED comma AC equals AE space... left parenthesis tangents space drawn space from space an space external space point space to space the space circle space are space equal right parenthesis AD equals AD space... left parenthesis common space side right parenthesis CD equals DE equals straight r space... left parenthesis radii space of space the space same space circle right parenthesis rightwards double arrow increment ACD space approximately equal to space AED space... left parenthesis SSS space congruence space criterion right parenthesis So comma space angle CAD equals angle DAE equals straight alpha over 2 space... left parenthesis cpct right parenthesis In space increment ACD comma sin straight alpha over 2 equals space CD over AD rightwards double arrow sin straight alpha over 2 equals space straight r over AD rightwards double arrow AD equals fraction numerator straight r space over denominator sin straight alpha over 2 end fraction rightwards double arrow AD equals straight r space cosec space straight alpha over 2.... left parenthesis straight i right parenthesis In space increment DAB comma sin space straight beta equals DB over AD rightwards double arrow AD equals fraction numerator DB over denominator sin space straight beta end fraction rightwards double arrow AD equals fraction numerator DB over denominator sin space straight beta end fraction.... left parenthesis ii right parenthesis From space left parenthesis straight i right parenthesis space and space left parenthesis ii right parenthesis comma space we space get straight r space cosec space straight alpha over 2 equals fraction numerator DB over denominator sin space straight beta end fraction rightwards double arrow DB equals straight r space cosec space straight alpha over 2 space sin space straight beta rightwards double arrow DB equals straight r space sin space straight beta space cosec space straight alpha over 2 So comma space the space height equals straight r space sin space straight beta space cosec space straight alpha over 2 Hence space proved. end style
Answered by Rebecca Fernandes | 14 Feb, 2017, 10:32: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
ABCD is a rectangle in which diagonal AC is equals to 17 cm angle BCA is equals to thitha and sin theta is equals to 8/17 find the area of rectangle ABCDE (ii) the perimeter of rectangle ABCD
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
the poles AB and CD of different heights are standing vertically on the ground level from a point P on the line joining the foots of the pole on the level of ground the angle of elevation to the top of the pole are founded to be complementary the of the CD and the distance PD 20√3m and 20m respectively if the BP is 10m then find the length of AB and the distance AC between the tpo of the poles
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
√1+sin A/√1-sin A
Asked by vn3950372 | 18 Mar, 2024, 08:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
from the top of your vertical building of 350 m height on a level ground the angle of depression on of an object on the same ground is observed to be 60 degree find the distance of the object from the foot of the building
Asked by jayashreelatha04 | 17 Mar, 2024, 05:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
trigonometry
question image
Asked by vk952384 | 09 Mar, 2024, 11:34: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
find the value of cos20 if 2sin20 is root 3
Asked by gauravgupta.20008 | 03 Feb, 2024, 05:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
6. A is an acute angle in right triangle, right angled at B then value of (sinA + CosA) is ( a) Greater than (b) less than 1 (c) equal to 1 (d) depends on value of A
Asked by sathwicksathwick06 | 01 Feb, 2024, 07:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
solution
question image
Asked by pankajmali55 | 25 Jan, 2024, 07:51: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Q1. Ina DABC, LB=90^{\circ} If AB=2cm and AC=3cm Find Sin A.
Asked by tanujmaan58 | 18 Jan, 2024, 08:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prove thar tan a-sin a/tan a+Sina, = sec a-1/sec A+1
Asked by balu162 | 16 Jan, 2024, 07:10: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×