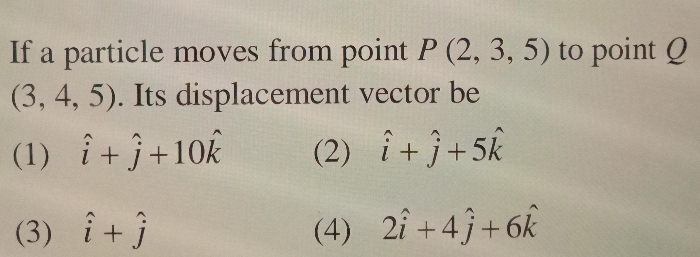a police inspector in a jeep is chasing a pickpocket on a straight road. the jeep is going with maximum speed v(assumed uniform). the pick pocket rides on the motor cycle of a waiting friend when the jeep is at a distance of 'd' away, the motorcycle starts with a constant acceleration a. show that the pick pocket will be caught if "v" is equal to or greater than "root over 2ad"

You might have studied quadratic equations, right? For a given quadratic equation, if you have to determine the roots are real, then you use that Discriminant (D) >=0

 

Here also, in this case, since we have a quadratic equation in t 

at^2 -2vt+2d = 0

 

And now, for the pick pocket to be caught, this equation should result in a real value of t. Hence, D for that matter needs to be greater than or equal to 0. 

 

Now, for a given quadratic equation, ax^2 + bx+c = 0, 

D  = b^2 - 4ac

 

So, in the above quadratic equation, b = -2v and a = a and c = 2d

 

Hence D = (-2v)^2 - 4*a*2d >=0

4v^2 -8ad >=0

v^2>=2ad

v>=sqrt(2ad)

 

Hence proved.