Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

A piece of gold (p=19.3 g/cm3) is suspected to be hollow from inside. It weighs 77.2 g in air and 71.2 g in water. What is the volume of hollow portion of the gold?
 
 



Asked by Jerlin George | 23 Nov, 2014, 12:02: PM
answered-by-expert Expert Answer
Given that the density of gold =19.3 g/cm3
Mass of gold piece in air =77.2 g
So volume of the gold piece will be:
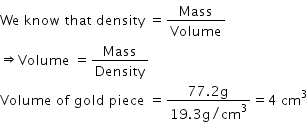
begin mathsize 14px style We space know space that space density space equals Mass over Volume rightwards double arrow Volume space equals Mass over Density Volume space of space gold space piece space equals fraction numerator 77.2 straight g over denominator 19.3 straight g divided by cm cubed end fraction equals 4 space cm cubed end style
Given that the mass of the gold piece in water =71.2 g
The apparent loss in weight of the gold in water will be equal to the weight of the water displaced by the gold piece.
Apparent loss of weight = 77.2g - 71.2 g =6 g
So the weight of water displaced by the gold piece = 6 g
Volume of water displaced =mass of water displaced / density of water
Volume of water displaced = 6g / 1 g/cm3 = 6 cm3
Volume of the gold piece = 4 cm3 and volume of water displaced by the gold piece= 6 cm3
As Volume of the gold piece is less than volume of water displaced by the gold piece we can say that the gold piece is hollow inside
Therefore the volume of hollow portion of the gold piece = volume of water displaced by the gold piece - Volume of the gold piece 
i.e. 6 cm3 - 4 cm3  = 2 cm3
Volume of hollow portion of gold = 2 cm3 .
Answered by Jyothi Nair | 23 Nov, 2014, 08:35: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Physics
Why do we feel light on our feet when standing in a swimming pool with water up to our armpits ?
Asked by mailtoparvathyprajith | 08 Feb, 2024, 12:13: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
what is density?
Asked by kaushik3199 | 26 May, 2021, 01:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
When a piece of cork is put into the water it starts floating on the surface of water due to the upward buoyant force from water.
Asked by sailavanya000 | 17 Dec, 2020, 04:09: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
you are provided with a piece of rock and common laboratory equipments.how will you proceed to find its density.  
Asked by dkhuntia78 | 22 Jul, 2020, 02:34: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
what are fluids?
Asked by swatipuspapatel | 19 Jul, 2020, 11:28: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
solution
question image
Asked by rohitkasbe11 | 20 Mar, 2020, 12:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
What is the unit of density?
Asked by sandhyaprasad100 | 08 Jan, 2020, 11:33: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
What happens if the bouyant force of liquid is equal to or greater than or less than the solid object which is to be immersed into the liquid
Asked by saradamahapatra9999 | 28 Dec, 2019, 09:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
what is the relationship between boyant force and displaced water
Asked by arpitchaudhary123 | 20 Nov, 2019, 03:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
pressure at certain depth in river water is p1.,same depth in sea water is p2.which of following is correct? a)p1=p2 b)p1>p2 c)p1<p2 d)p1-p2=atmospheric pressure
Asked by arajeevshashank | 19 Nov, 2019, 07:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×