CBSE Class 9 Answered
a particle is moving in a straight line with initial velocity U and uniform acceleration a. If the sum of the distances travelled in 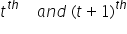 seconds in 100cm , then its velocity after t seconds in cm/s is
seconds in 100cm , then its velocity after t seconds in cm/s is
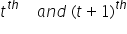 seconds in 100cm , then its velocity after t seconds in cm/s is
seconds in 100cm , then its velocity after t seconds in cm/s is
Asked by Petulla Mishra | 04 Nov, 2015, 10:16: AM
We know that the distance travelled in nth second of uniformly accelerated motion is:

where u is the initial velocity and a the uniform acceleration of the body.
In this case given that the sum of distances travelled in tth & (t+1)th second is 100 cm.
i.e.
St + St+1 = 100
If the particle is moving with initial velocity U and uniform accerleration a, then the distance travelled by the particle in tth second can be written as:

Given that St + St+1 = 100
Substituting eqn (1) and (2), we get,

According to the equation of motion, we know that v = u+at, where v is the final velocity, u is the initial velocity, a the acceleration and t the time.
So comparing the equation U+at =50 with the the equation of motion v= u+at, we get that the final velocity of the particle at t second = 50 cm/s.
Answered by Faiza Lambe | 04 Nov, 2015, 11:18: AM
Application Videos
Concept Videos
CBSE 9 - Physics
Asked by janhavisoni2099 | 02 Oct, 2023, 05:20: PM
CBSE 9 - Physics
Asked by sagrawal0081 | 18 Aug, 2023, 05:04: PM
CBSE 9 - Physics
Asked by ketkiparasgandhi | 05 Jul, 2023, 08:02: PM
CBSE 9 - Physics
Asked by adityatripathi84418 | 02 May, 2023, 10:29: PM
CBSE 9 - Physics
Asked by rsaranya658 | 30 Jun, 2022, 02:44: PM
CBSE 9 - Physics
Asked by poornimaram165 | 21 Jun, 2022, 09:16: PM
CBSE 9 - Physics
Asked by saanidhyapatil | 16 Feb, 2022, 01:23: PM
CBSE 9 - Physics
Asked by pradeepkumarbhegde5175 | 12 Jan, 2022, 11:25: PM
CBSE 9 - Physics
Asked by debargharoy057 | 25 Sep, 2021, 09:48: AM