CBSE Class 11-science Answered
A class got 48 distinctions in maths, 25 in physics and 30 in chemistry. If these went to a total of 68 students and only 5 students got distinctions in all the three subjects, how many students got distinctions in exactly two of the three subjects?
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
Let M, P and C denote the set of students who got distinction in maths, physics and chemistry respectively.
Then n(M) = 48, n(P) = 25, n(C ) = 30
n(M 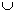 P
P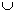 C) = 68 and n(M
C) = 68 and n(M 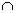 P
P 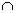 C) = 5
C) = 5
Therefore,
n(M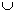 P
P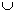 C) = n(M) + n(P) + n(C) – n(M
C) = n(M) + n(P) + n(C) – n(M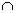 P) – n(M
P) – n(M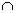 C) - n(P
C) - n(P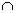 C) + n(M
C) + n(M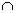 P
P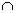 C)
C)
Now consider the following Venn diagram:
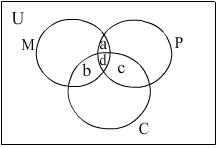
Here,
a denotes the number of students who got distinction in maths and physics only.
b denotes the number of students who got distinction in maths and chemistry only.
c denotes the number of students who got distinction in physics and chemistry only.
d denotes the number of students who got distinctions in all the three subjects.
Thus, d = n(M  P
P  C) = 5 and
C) = 5 and
a + d + b +d + c + d = 40
Therefore, a + b + c = 25
Answered by | 04 Jun, 2014, 03:23: PM
Concept Videos
CBSE 11-science - Maths
Asked by Topperlearning User | 17 Apr, 2014, 11:58: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 17 Apr, 2014, 11:45: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 17 Apr, 2014, 01:18: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 31 Aug, 2016, 11:28: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 17 Apr, 2014, 11:47: AM


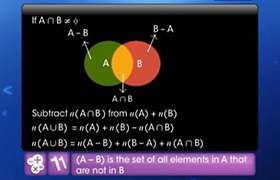

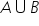 has 40 elements, A has 30 elements and B has 20 elements, how many elements does the shaded region have?
has 40 elements, A has 30 elements and B has 20 elements, how many elements does the shaded region have?