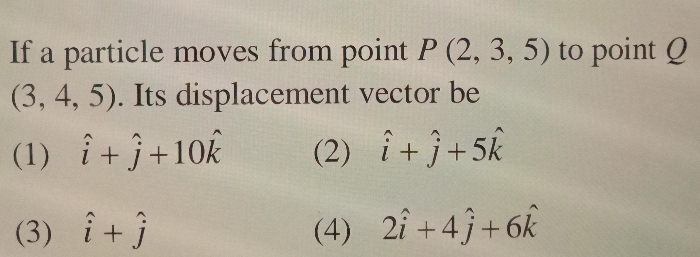Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

A bullet fired into a large block of wood of uniform resistance, hits the block with a velocity of 48 m/s.It penetrates a distance of 60 cm and the velocity is then reduced to 24m/s. It then penetrates a further distance of (in cm)?
Asked by aruni_maiyer | 11 Jul, 2010, 09:27: PM
answered-by-expert Expert Answer
Let the initial velocity be u and constant retardation be a.
Then
v2 = u2 - 2aS
(24)2 = (48)2 - 2a(60)
or, 120a = 2304 - 576 = 1728

or, a = 14.4 m/s2

Let the bullet covers a total distance of x .
Then using the same acceleration we get:

02 = u2 - 2ax.
 0 = 2304 - (2x14.4)(x)

x = 2304/(2x14.4) = 80cm.

So, the bullet covers a total a 80 cms into the target or the bullet goes furthur by 20 cms.
 
Hope this helps,
Team Topper
Answered by | 12 Jul, 2010, 04:11: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Physics
Q17. The velocity time relation of an electron starting from rest is given by v = kt where k = 6m / (s ^ 2) Calculate the distance traversed in 2 sec. 122
Asked by om636694 | 04 Mar, 2024, 09:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
1. Explain path length and displacement with illustrations and distinguish them. 2. Define uniform velocity of an object moving along a straight line. What will be the shapes of position-time and velocity-time graphs of such a motion? Find the distance travelled by the uniformly accelerated object in one dimension in nth second. Draw velocity-time graph of a uniformly accelerated motion in one dimension and explain that the distance travelled is equal to the area under velocity-time graph. ted motion deduce the equations of motion in (i) From the velocity-time graph of uniform accelerated motion. velocity and time (ii) distance and time (iii) distance and velocity. Show that the vector addition of two vectors is different from scalar addition of two scalars. 7. What vectors. zero vector? How can you obtain zero vectors? Give examples and properties of zero It is easier to pull than to push a lawn roller. Explain with diagram. State triangle law vector. vector addition. Find analytically the magnitude direction resultant 10. State parallelogram law of vector addition. Find analytically the magnitude and direction of resultant vector, when (i) two vectors other. parallel to each-other (ii) two vectors perpendicular to each- 11. What a projectile? Give its examples. Show projected horizontally from a certain height.
question image
Asked by amarjeetmandal290 | 19 Feb, 2024, 10:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
state and prove law of conservation of energy in case of a freely falling bady
Asked by dhanapolla | 28 Jan, 2024, 10:40: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
if the linear momentum of a body is increased by 10% what will be the percentage change in it's kinetic energy
Asked by santoshyadav6673633 | 26 Jan, 2024, 04:55: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
If a particle moves from point P(2,3,5) to Q(3,4,5). Its displacement vector be
question image
Asked by manjusrihalder395 | 07 Jan, 2024, 09:55: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
a bullet travelling with speed of 16m/s penetrates a tree trank come to rest in 0.4m find the time taken during retard
Asked by rahmanshah8572 | 29 Dec, 2023, 08:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
obtain equations of motion for constant acceleration using calculus method
Asked by klvnsnthl | 25 Dec, 2023, 07:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
the angle of inclination of an inclined plane is 60 degrees. Cooefificent of friction between 10kg body on it and it's surface is 0.2,g= 10ms secnod squre. The acceleration of the body in meter ler second is
Asked by pothulasubbarayudu | 25 Dec, 2023, 06:58: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
what is elevators
Asked by neerajchaurasiya651 | 10 Dec, 2023, 09:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
a mass of 0.1 kg falls freely under the action of gravity find the force acting on it it's momentum and kinetic energy after 10 sec ?
Asked by debasishbarik2006 | 17 Nov, 2023, 07:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×