Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

A 5 m pole long ladder is placed leaning forward on a vertical wall , such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m toward the wall then find the distance by which the top of the ladder slide upwards on the wall.
Asked by vans75a | 31 Jul, 2015, 08:09: PM
answered-by-expert Expert Answer
 
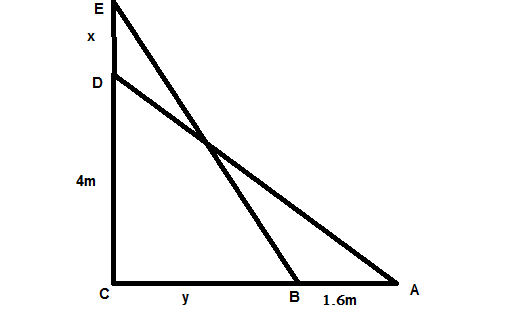
Initially AD is the ladder of length 5 m which reaches the wall at the point D which is 4 m high from C. 
When we move it 1.6m towards the wall, now it's at point B in the figure. The topp of the ladder now reaches point E on wall. 
We have to find the distance DE. In the figure, DE=x m and BC=y m. AD=BE=5 m (length of the ladder)
In the right angled triangle ACD, we have
A D squared equals A C squared plus C D squared space rightwards double arrow 5 squared equals left parenthesis 1.6 space plus space y right parenthesis squared space plus space 4 squared rightwards double arrow left parenthesis 1.6 space plus space y right parenthesis squared equals 5 squared minus space 4 squared rightwards double arrow left parenthesis 1.6 space plus space y right parenthesis squared equals 9 rightwards double arrow 1.6 space plus space y equals 3 rightwards double arrow y equals 1.4 space m
Similarly, in the right angled triangle BCE, we have
B E squared equals B C squared plus C E squared rightwards double arrow 5 squared equals y squared plus open parentheses 4 plus x close parentheses squared rightwards double arrow 5 squared equals 1.4 squared plus open parentheses 4 plus x close parentheses squared rightwards double arrow open parentheses 4 plus x close parentheses squared equals 5 squared minus 1.4 squared rightwards double arrow open parentheses 4 plus x close parentheses squared equals 3.6 cross times 6.4 space space left parenthesis u sin g space a squared minus b squared equals open parentheses a plus b close parentheses cross times open parentheses a minus b close parentheses right parenthesis rightwards double arrow open parentheses 4 plus x close parentheses equals square root of 3.6 cross times 6.4 end root rightwards double arrow 4 plus x equals 4.8 rightwards double arrow x equals 4.8 minus 4 equals 0.8 space m
Hence, the top of the ladder slides upward by a distance of 0.8 m.
Answered by satyajit samal | 02 Aug, 2015, 12:14: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
find area
question image
Asked by kashinigam382 | 05 Jan, 2024, 04:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
what is triangle
Asked by suryapalsinghgoudmahirajbanna | 17 Sep, 2023, 10:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
hi sir can u please say hoe to find the angles of trianglr wheather it is a right angle                                                                                                                      
Asked by bnarayanamstr | 03 May, 2023, 10:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
plz solve urgently plz:
question image
Asked by savitamahajan202 | 30 Dec, 2022, 12:51: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
give answer
question image
Asked by kumarjogesh746 | 28 Dec, 2022, 07:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Answer of the question given below
question image
Asked by bhu.joshi54 | 04 Jul, 2022, 08:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
the perimeter of two similar triangles are 25cm and 15cm respectively. if one side of the first triangle is 9cm,what is the corresponding side of the other triangle
Asked by bhu.joshi54 | 16 Jun, 2022, 07:56: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
triangle
Asked by ankitamityadav65 | 06 Apr, 2022, 02:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
 in a equilateral triangle, d is a side on BC such that BD is 1/3 BC Prove that 9(AD)^2=7(AB)^2
Asked by dishapalnati82 | 24 Nov, 2021, 09:30: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Question is in image
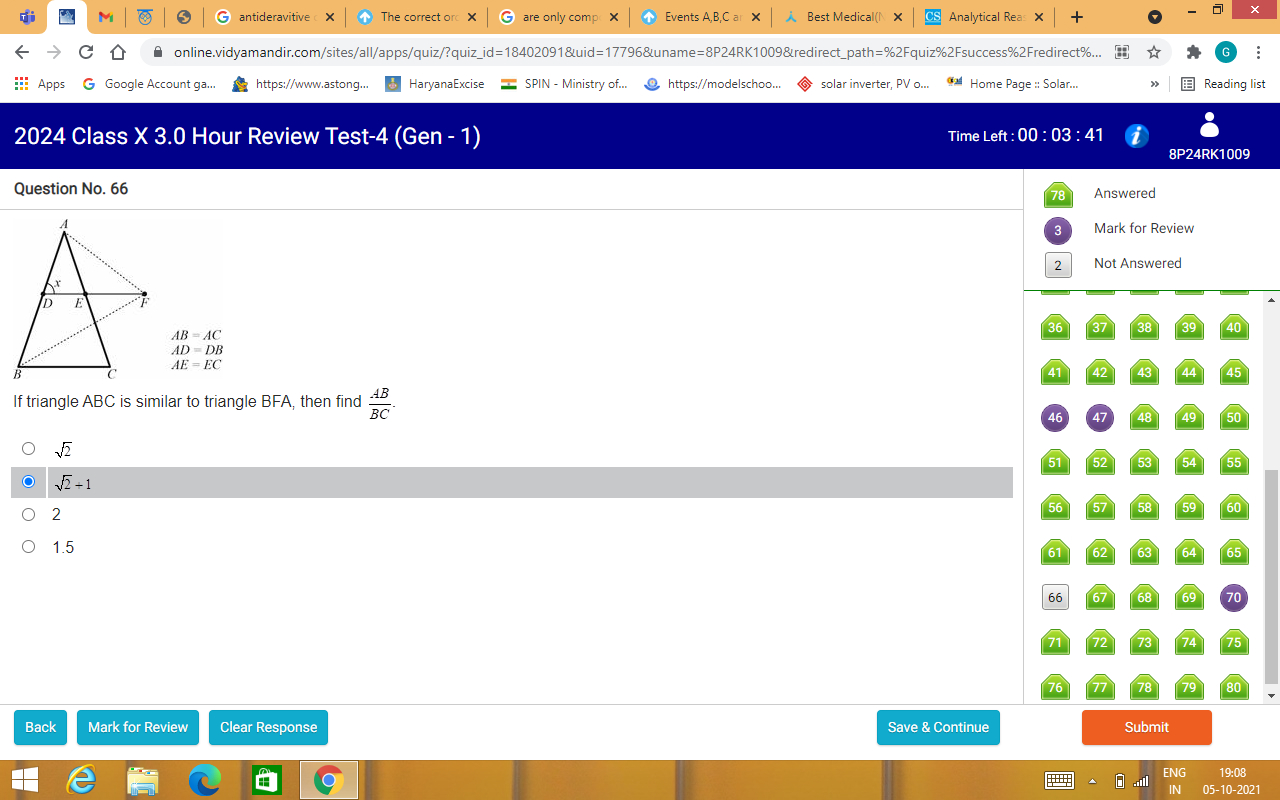
question image
Asked by psinghaladv | 05 Oct, 2021, 07:49: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×