A 4 μF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 2μF capacitor. How much electrostatic energy of the first capacitor is lost in the heat and electromagnetic radiation?
Asked by Topperlearning User | 22nd Apr, 2015, 08:40: AM
Expert Answer:
Capacitance of a charged capacitor, C1 = 4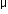 
F = 4 × 10-6 F
Supply voltage, V1= 200 V
Electrostatic energy stored in C1is given by,
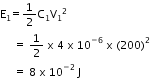
Capacitance of an uncharged capacitor, C = 2 μF = 2 × 10-6 F
When C2 is connected to the circuit, the potential acquired by it is V2.
According to the conservation of charge, initial charge on capacitor C1 is equal to the final charge on capacitors, C1 and C2.
therefore, V2 (C1 + C2) = C1V1
V2 × (4 + 2) × 10-6 × 200
V2 = 
V
Electrostatic energy for the combination of two capacitors is given by,
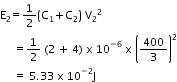
Hence, amount of electrostatic energy lost by capacitor C1
= E1 - E2
= 0.08 - 0.0533 = 0.0267
= 2.67 x 10-2 J
Answered by | 22nd Apr, 2015, 10:40: AM
Concept Videos
- Two charges 2microcoulmb and-2microcoulmb are placed at A and8.5 apart depict equipotential surface of the system
- An alpha particle is accelerated through a potential difference of 2000v what will be the increase in energy in electron volt
- If one of the two electrons of a H2 molecule is removed, we get a hydrogen molecular ion
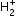. In the ground state of an , the two protons are separated by roughly 1.5
, and the electron is roughly 1 from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.
- The plates of a parallel plate capacitor have an area of 90 cm2 each and are separated by 2.5 mm The capacitor is charged by connecting it to a 400 V supply How much electrostatic energy is stored by the capacitor? View this energy as stored in the electrostatic field between the plates, and obtain the energy per unit volume u. Hence arrive at a relation between u and the magnitude of electric field E between the plates.
- Write an expression for the electrostatic potential energy in terms of the electric field.
- How much work is required to be done to separate the charges of a dipole till infinity with Q ± 7μC and r = 0.18 m?
- What is the potential at a point 6 × 10-15 m away from a proton? What will be the potential energy of a system, if another proton is brought to a distance 2 × 10-15 m from it?
- How much work has to be done to maintain electric dipole with moment 6 x 10-8 cm and angle 60o in an electric field of magnitude 1.2 x 104 N/C?
- (a) Depict the equipotential surfaces for a system of two identical positive point charges placed a distance 'd' apart.
(b) Deduce the expression for the potential energy of a system of two point charges q1 and q2 brought from infinity to the points
respectively in the presence of external electric field 
.
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change