CBSE Class 10 Answered
Dear Student,
Let cost of each chair = Rs. x
and cost of each table = Rs. y
According to the statement, 4 chairs and 3 tables cost Rs. 2100
4 × (cost of one chair) + 3 × (cost of one table) = Rs. 2100
So, we get an equation
4x + 3y = 2100 ……...... (i)
Also, 5 chairs and 2 tables cost Rs.1750
So we get another equation
5x + 2y = 1750 ……….. (ii)
We will solve equations (i) and (ii) to get the answer
Let us solve the two equations using elimination method
2 × equation (i) gives
8x + 6y = 4200 ………………………… (A)
And 3 × equation (ii) gives
15x + 6y = 5250 ……………………….. (B)
Subtracting (A) from (B), we get
15x + 6y – 8x – 6y = 5250 – 4200
7x = 1050
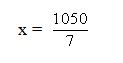
So x = 150
Substituting this value of x in equation (ii), we get
5(150) + 2y = 1750
750 + 2y = 1750
2y = 1750 – 750
2y = 1000
So y = 500
Hence, cost of each chair = Rs. 150
and cost of each table = Rs. 500
Regards
Team
Topper Learning

