CBSE Class 9 Answered
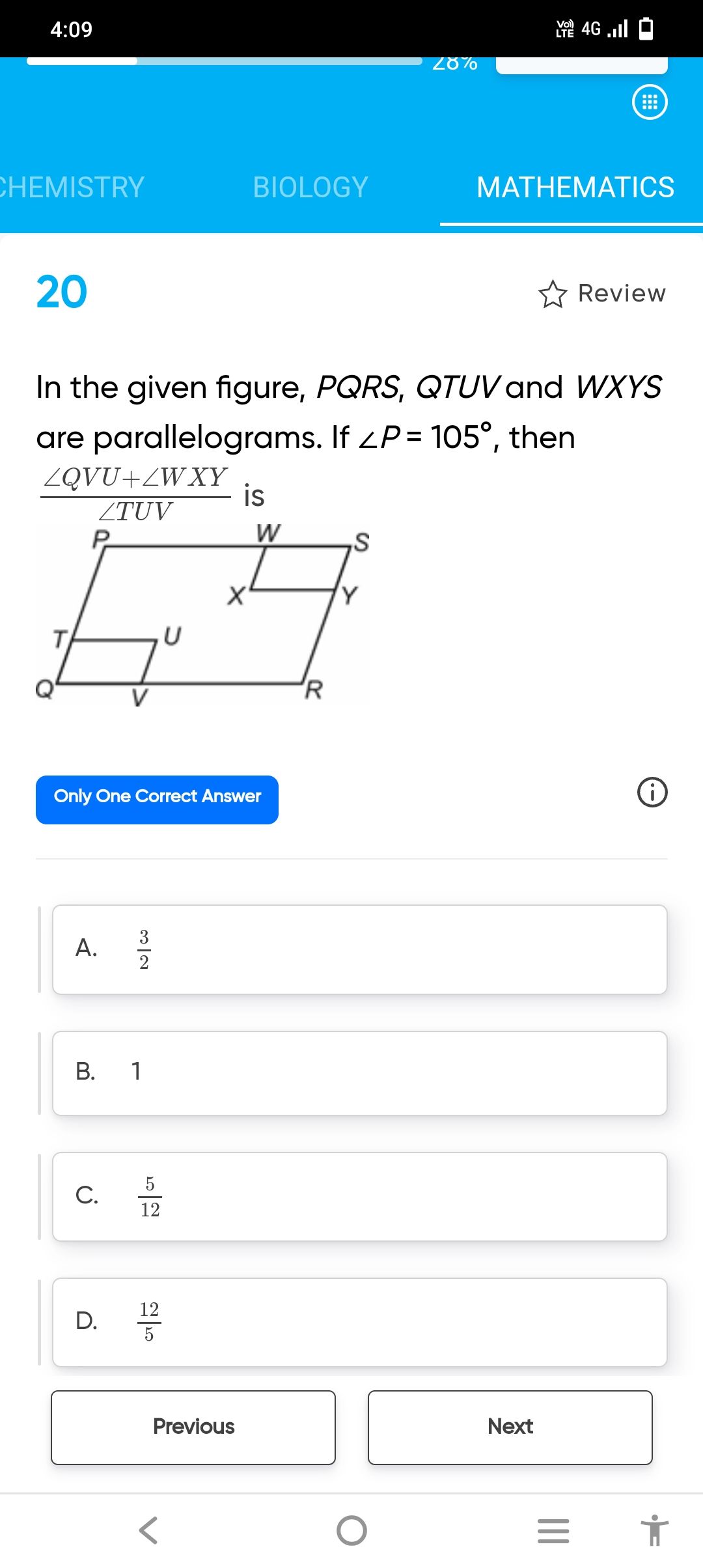
4) Given a rectangle ABCD and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Length of diagonal of a rectangle is 8cm. Then the quadrilateral PQRS is a
(a) parallelogram with adjacent sides 4cm and 6cm
(b) rectangle with adjacent sides 4cm and 6cm
(c) rhombus with side 4cm
(d) square with side 4cm
Asked by Madhuchhanda Chakraborty | 25 Dec, 2013, 03:11: PM
Expert Answer
Consider the following figure.
Let the length and the breadth of the rectangle be 2a and 2b units.
From Pythagoras Theorem, we have,
In ΔABC,
P and Q are the mid-points of AB and BC respectively.
∴ PQ || AC and PQ = AC (Mid-point theorem) ... (1)
Similarly in ΔADC,
SR || AC and SR = AC (Mid-point theorem) ... (2)
Clearly, PQ || SR and PQ = SR
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to
each other, it is a parallelogram.
P and Q are the mid-points of AB and BC respectively.
∴ PQ || AC and PQ = AC (Mid-point theorem) ... (1)
Similarly in ΔADC,
SR || AC and SR = AC (Mid-point theorem) ... (2)
Clearly, PQ || SR and PQ = SR
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to
each other, it is a parallelogram.
Also we have 
(linear pair) and 
.
(linear pair) and .In the parallelogram PQRS all the sides are equal to 
and the diagonals are perpendicular and hecne PQRS is a rhombus.
and the diagonals are perpendicular and hecne PQRS is a rhombus.Since the diagonal AC = 8 cm (given), we have
Thus, PQRS is a rhombus with side 4 cm.
Hence, (c) is the correct option.
Answered by Vimala Ramamurthy | 26 Dec, 2013, 09:12: AM
Application Videos
-
Relation between Parallelogram and Triangle ...
This video explains the relation between the parallelogram and the triangle... -
Properties of a Parallelogram
This video contains a question which is solved using the property of a para... -
Use of Mid-point theorem
The video explains case study based type of question which is based on t...
-
Properties of Parallelogram
The video explains case study based type of question which is based on t...
-
Properties of quadrilateral
The video explains case study based type of question which is based on t...
Concept Videos
-
About relation between opposite angles in a parallelogr ...
Relation between opposite angles in a parallelogram. Explore the conditions... -
Relation between the diagonals of a parallelogram ...
Establish the relation between the diagonals of the parallelogram. Conditio... -
Mid Point Theorem
This video explains the Mid - Point theorem and its converse for a triangle... -
Types and Angle Sum Property
. Definition of Quadrilateral & special quadrilaterals: rectangle, square,... -
Parallelograms: Basic Properties
Parallelograms:Basic Properties
CBSE 9 - Maths
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by sagrawal0081 | 31 Aug, 2023, 07:24: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by jahnavinehra | 03 Jul, 2022, 11:19: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by abhiroy1462 | 16 Apr, 2022, 02:25: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by abdullahzedane2008 | 28 Mar, 2022, 12:11: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by sanskritiraghudev | 19 Feb, 2022, 09:38: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by varundhawan | 31 Jan, 2022, 10:41: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM
ANSWERED BY EXPERT
