CBSE Class 9 Answered
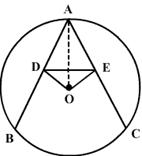
1.In the figure, OD is perpendicular to chord AB of a circle whose centre is O. If BC is diameter; prove that CA = 2OD.
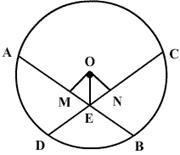
2. l is a line intersecting two concentric circles having common centre O, at A, B, C and D. Prove that AB = CD.
3. AB and CD are equal chords of a circle whose centre is O. When produced, these chords meet at E. Prove that EB = ED.
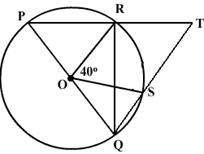
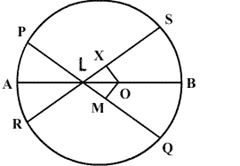
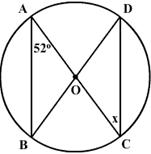
4. If O be the centre of the circle, find the value of �x� in each of the following figures.
5. Prove that equal chords of a circle subtend equal angles at the centre.
6. The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord. Prove it.
7. Prove that equal chords of a circle (or congruent circles) are equidistant from the centre (or centres).
8. In the figure, OD is perpendicular to the chord AB of a circle with centre O. If BC is a diameter, show that AC || OD and AC = 20D.
Hint: ∴ OD ⊥ AB therefore; D is the mid-point of AB.
9. If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.
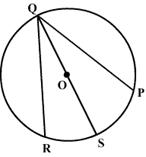
10. Show that the angles in the same segment of a circle are equal.
Asked by aahnik.mohanty | 30 Dec, 2017, 10:21: AM

Note: Please post one query at a ime.
Answered by Rashmi Khot | 30 Dec, 2017, 03:48: PM
Concept Videos
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:15: AM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 08:51: AM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:17: AM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:25: AM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 08:49: AM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:22: AM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Aug, 2017, 08:40: AM
CBSE 9 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:24: AM





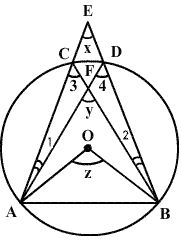
 XPZ is equal to twice the sum of
XPZ is equal to twice the sum of 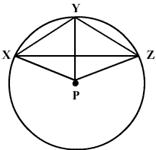
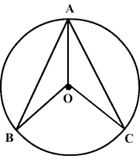
 ADE is an isosceles triangle.
ADE is an isosceles triangle.