Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

1) why f(x) is continuous only for Closed interval [a, b] ?
 
2) why f(x) is differentiable only for open interval (a, b) why not for closed interval  ?
 
( these questions r related to condition for rolle's theorem n LMVT )
 
Plz explain in detail
Asked by Ritusha Kulkarni | 09 Jul, 2015, 07:27: PM
answered-by-expert Expert Answer
(1) Continuity at end points is necessary for rolle's theorem to be valid. 
Let us see one example where a function is not continuous at end points of an interval.
 
 
For the above function f(x)=1 for x< or equal to 1
                             f(x)=ex for 1<x<2
                             f(x)=1 for x > or equal to 2
The function is continuous in the open interval (1,2). It is differentiable in the open interval (1,2). f(1)=f(2). 
It satisfies all conditions of Rolle's theorem except continuity at end points. The function is not continuous at either x=1 or x=2. 
We can observe that Rolle's theorem is not valid here- we don't get any point 'c' in the interval (1,2) for which f'(c)=0. 
So, continuity at end points is important for the Rolle's theorem. Without that we will not always get a point 'c' in the interval for which f'(c)=0
 
(2) Differentiability at end points is not necessary for Rolle's theorem to be valid. The function may or may not be differentiable at end points of the interval chosen.
Again let us see one example below.
 
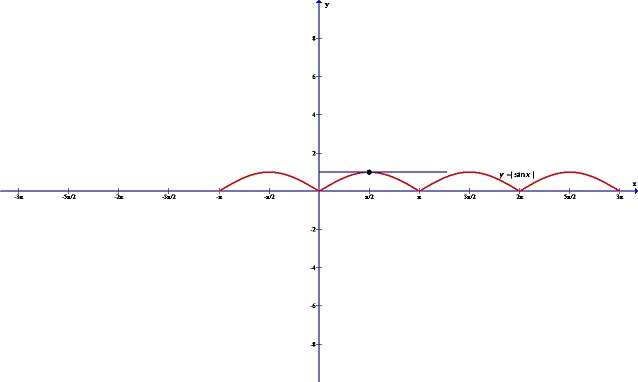
The above function f(x)=|sinx| is continuous in the closed interval [0, pi]
It is differentiable in the open interval (0, pi). (not differentiable at either '0' or 'pi')
f(0)=f(pi) = 0
We observe at x=pi/2 , f'(pi/2) = 0 . Hence, we get one point in the interval (0, pi) for which derivative is zero. Hence, Rolle's theorem is valid here. 
So, Rolle's theorem can be valid even if the function is not differentiable at end points. Hence, we have f(x) differentiable in open interval (a,b) in the theorem.
 
Answered by satyajit samal | 10 Jul, 2015, 11:03: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
Discuss the applicability of Rolle’s theorem for the following function on the indicated interval: f(x) = |x| on [–1, 1]
Asked by Topperlearning User | 04 Aug, 2014, 03:57: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Discuss the applicability of Rolle’s theorem for the following function  on the indicated interval : f (x) = 3 + (x – 2)2/3 on [1, 3]
Asked by Topperlearning User | 04 Aug, 2014, 04:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Discuss the applicability of Rolle’s theorem for the following function on the indicated interval: f (x) = tan x on  [0, p]
Asked by Topperlearning User | 04 Aug, 2014, 04:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Discuss the applicability of Rolle’s theorem on the function f (x) = open curly brackets table attributes columnalign left columnspacing 1.4ex end attributes row cell straight x plus 1 comma end cell cell when space 0 less or equal than straight x less or equal than 1 end cell row cell 3 minus straight x comma end cell cell when space 1 less or equal than straight x less or equal than 2 end cell end table close
Asked by Topperlearning User | 04 Aug, 2014, 04:11: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Verify Rolle’s theorem for the function f (x) = x2 – 5x + 6 on the interval [2, 3].
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Verify Rolle’s theorem for the function f (x) = (x – a)m (x – b)n on the interval [a, b], where m, n are positive integers.
Asked by Topperlearning User | 05 Aug, 2014, 08:38: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Verify Rolle’s theorem for the function f (x) = square root of 4 minus straight x squared end root on [– 2, 2].
Asked by Topperlearning User | 04 Aug, 2014, 03:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Verify Rolle's theorem for the function f (x) = log space open curly brackets fraction numerator straight x squared plus ab over denominator straight a left parenthesis straight a plus straight b right parenthesis end fraction close curly brackets on [a, b], where 0 < a < b.
Asked by Topperlearning User | 04 Aug, 2014, 03:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Verify Rolle’s theorem for each of the following functions on indicated intervals : f(x) = sin x + cos x – on open square brackets 0 comma straight pi over 2 close square brackets
Asked by Topperlearning User | 04 Aug, 2014, 04:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Verify Rolle's theorem for each of the following functions on indicated intervals : f (x) = sin x –  sin 2 x on [0, p]
Asked by Topperlearning User | 04 Aug, 2014, 04:35: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×