CBSE Class 12-science Answered
(i)
Reflexivity: Let (a, b) be an arbitrary element of N x N. Then in this case:
(a, b) N x N
=> a, b N
=> a + b = b + a
=> (a, b) R (a, b)
Hence (a, b) R (a, b) for all (a, b) 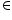 N x N. So, R is reflexive on N x N.
N x N. So, R is reflexive on N x N.
Symmetry: Let (a, b), (c, d) 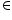 N x N be such that (a, b) R (c, d). Then:
N x N be such that (a, b) R (c, d). Then:
(a, b) R (c, d)
=> a + d = b + c
=> c + b = d + a
=> (c, d) R (a, b)
Thus, (a, b) R (c, d) => (c, d) R (a, b) for all (a, b), (c, d)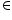 N x N
N x N
Hence R is symmetric on N x N
Transitivity: Let (a, b), (c , d), (e, f) 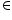 N x N such that (a, b) R (c, d) and (c, d) R (e, f).
N x N such that (a, b) R (c, d) and (c, d) R (e, f).
Then (a, b) R (c, d) => a + d = b + c
(c, d) R (e, f) => c + f = d + e
=> (a + d) + (c + f) = (b + c) + (d + e)
(ii)

Here, f(-1) = f(1) = 1 but -1 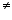 1
1
Thus, f is not one-one.
Also, -2 is in the co-domain R but is not the image of any element x in the domain R.
Thus, f is not onto.
Hence f is not bijective.
(iii)
For f to be invertible, we will prove that f is bijective.
Let x1, x2 R
Then f(x1) = f(x2)
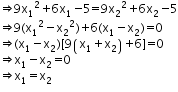
Thus, 'f' is one-one
Obviously, f:R ---> Range (f) is onto.
Thus, 'f' is bijective and hence invertible.













