ICSE Class 10 Answered

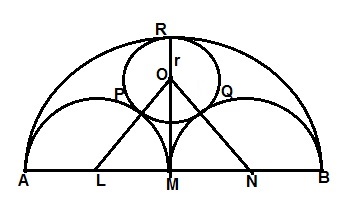
1) AB is a line segment and M is its mid-point .Three semi circles are drawn with AM, MB and AB as diameters on the same side of the line AB. A circle with radius r units is drawn so that it touches all the three semi circles .Show that AB=6 times r.

2) ABC is a right triangle with angle B=90 degree. A circle with BC as diameter meets hypotenuse AC at point D .Prove that (i) AC*AD=AB*AB. (ii)BD*BD=AD*DC.

3)In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisectors of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:(i)angle ONL+ angle  OML =180 degree. (ii) angle BAM =angle BMA. (iii)ALOB is a cyclic quadrilateral.

 4)In the given figure, PAT is a tangent to the circle with centre O, at point A on its circumference and is parallel to the chord BC. If CDQ is a line segment, show that :(i) angle BAP =angle ADQ.(ii) angle AOB = angle 2* angle ADQ.(iii) angle ADQ =angle ADB.