CBSE Class 11-science Answered
1 +1/1+2 +1/1+2+3 +.....+1/1+2+3+...n =2n/n+1.prove by principle of mathematical induction.
Asked by Akash Sundi | 15 Mar, 2012, 03:06: PM
P(n) = 1 + 1/(1+2) + ...... + 1/(1+2+3+ ... +n)
So P(1) = 1 , Put n =1 in 2n/(n+1) we get 1
thus P(1) is true , Now let P(k) is true
So P(k) = 1 + 1/(1+2) + ...... + 1/(1+2+3+ ... +k)
To Prove is P(k+1) is true that is P(k+1) = 2(k+1)/(k+2)
Now P(k+1) = 1 + 1/(1+2) + ...... + 1/(1+2+3+ ... +k) + 1/(1+2+3+ ... k+k+1)
= 2k/(k+1) + 1/{(k+2)(k+1)/2} [ sum of n terms = n(n+1)/2]
= 2k/(k+1) + 2/(k+2)(k+1)
= 2{k2 + 2k + 1}/(k+1)(k+2) = 2(k+1)/(k+2) = R.H.S.
Answered by | 15 Mar, 2012, 05:38: PM
Concept Videos
CBSE 11-science - Maths
Asked by keeruzzzzz | 11 Mar, 2020, 07:35: PM
CBSE 11-science - Maths
Asked by syedaliasad649 | 01 Oct, 2019, 07:07: PM
CBSE 11-science - Maths
Asked by lovemaan5500 | 02 Feb, 2019, 08:24: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 14 May, 2014, 03:21: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 07 Aug, 2014, 08:49: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 15 May, 2014, 10:48: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM







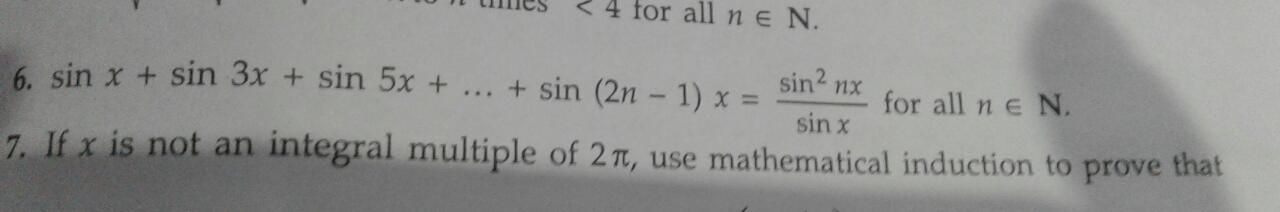
 n(3n-1)
n(3n-1)