CBSE Class 10 Answered
Show that there is no positive integer n for which √(n-1) +√(n+1) is rational.{In this question I am confused about the contradiction that any two perfect squares differ at least by 3. But some numbers like √2.25 & √4 have 1.5&2 whose difference is 0.5 . So how is it possible?}
Asked by Ananay | 05 Apr, 2017, 06:14: PM
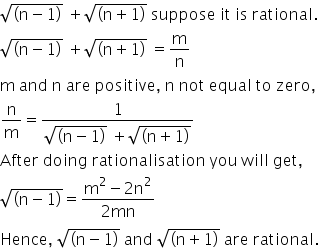
Answered by | 05 Apr, 2017, 06:25: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by aditikaldate7 | 21 Apr, 2024, 03:16: PM
CBSE 10 - Maths
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
CBSE 10 - Maths
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
CBSE 10 - Maths
Asked by rrajansinghakb199 | 08 Apr, 2024, 05:12: PM
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
CBSE 10 - Maths
Asked by muttenenimalleswarrao | 29 Mar, 2024, 08:32: PM
CBSE 10 - Maths
Asked by pathakvaishnavi9139 | 23 Mar, 2024, 10:45: AM
CBSE 10 - Maths
Asked by mustafahssn786 | 23 Mar, 2024, 06:25: AM