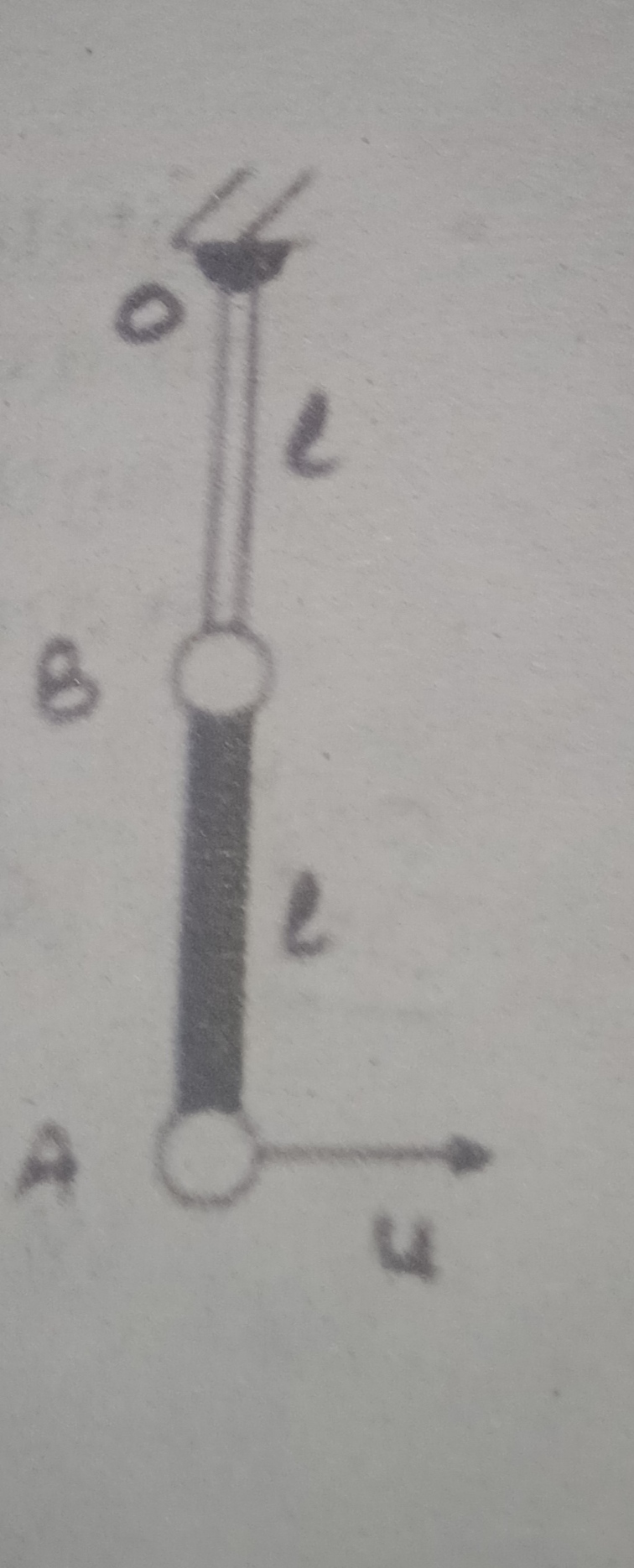Doubts and Solutions
OR
ICSE X - Maths
Asked by bhagvantingre | 24 Apr, 2024, 03:05: PM
CBSE XII Science - Physics
Asked by artabandhusahu85 | 24 Apr, 2024, 12:07: PM
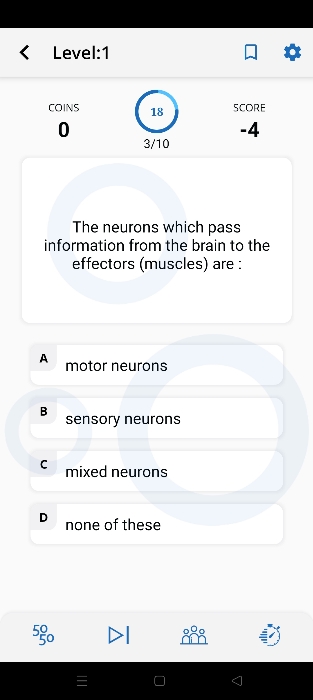
CBSE X - Biology
Asked by kunchalasrinivasaraosrinivasar | 23 Apr, 2024, 07:40: PM
CBSE XII Science - Physics
Asked by niharvijayvargiya5 | 23 Apr, 2024, 06:40: PM
CBSE VIII - Maths
Asked by gk9941740 | 23 Apr, 2024, 05:13: PM