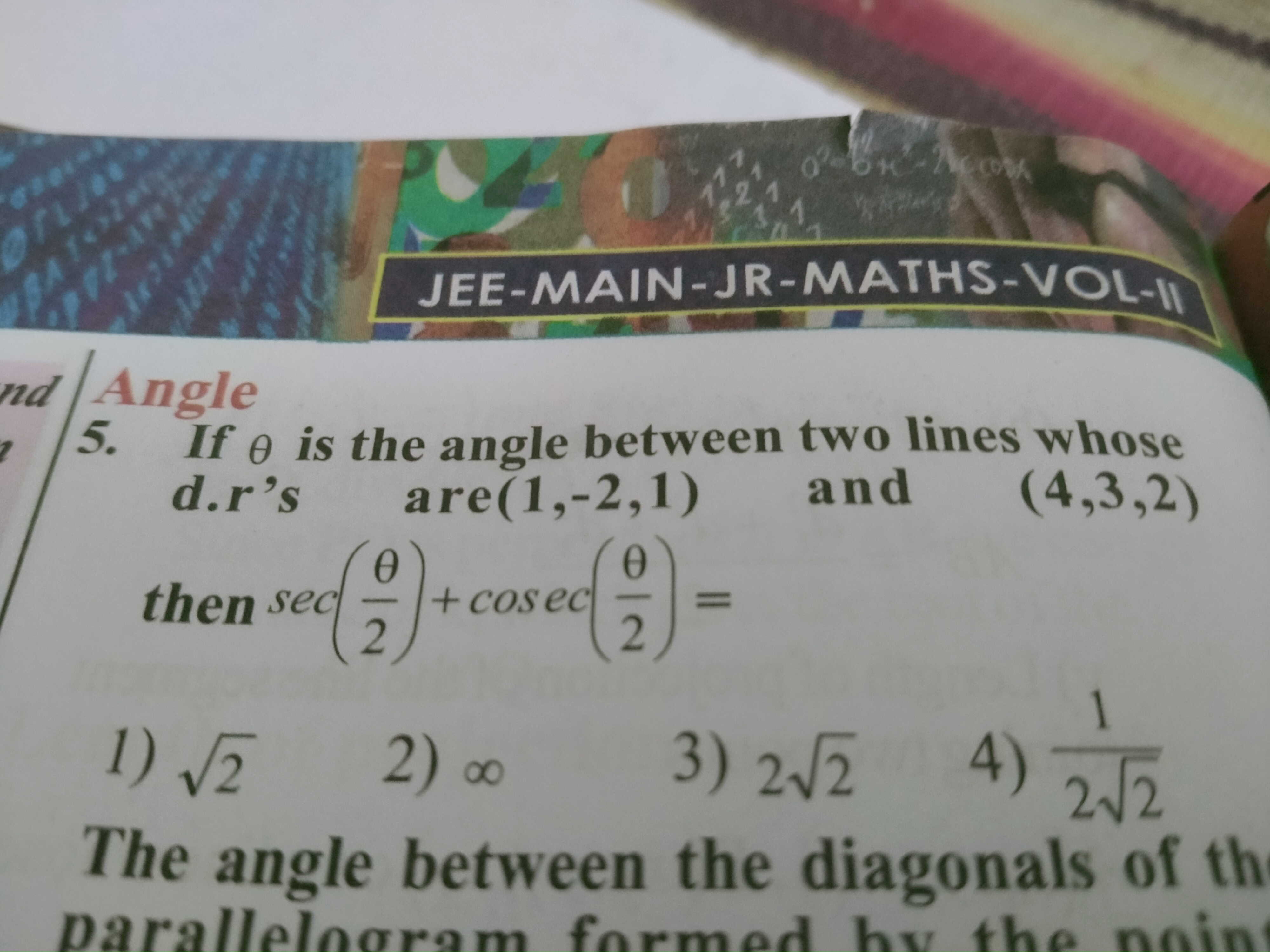Doubts and Solutions
OR
NEET NEET - Physics
Asked by praveenpriya000079 | 18 Apr, 2024, 07:24: AM
CBSE XII Science - Chemistry
Asked by hannamaryphilip | 17 Apr, 2024, 11:20: PM
CBSE XI Science - Physics
Asked by sheikhsaadat24 | 17 Apr, 2024, 09:41: PM
ICSE VII - Biology
Asked by arnabtoppo | 17 Apr, 2024, 09:28: PM
JEE Main - Chemistry
Asked by ashwinskrishna2006 | 17 Apr, 2024, 07:17: PM
NEET NEET - Biology
Asked by anandibastavade555 | 17 Apr, 2024, 07:08: PM
JEE Main - Maths
Asked by veerababukoppisettiveerababu3 | 17 Apr, 2024, 05:49: PM
NEET NEET - Physics
Asked by gouranshi84 | 17 Apr, 2024, 05:23: PM