Doubts and Solutions
OR
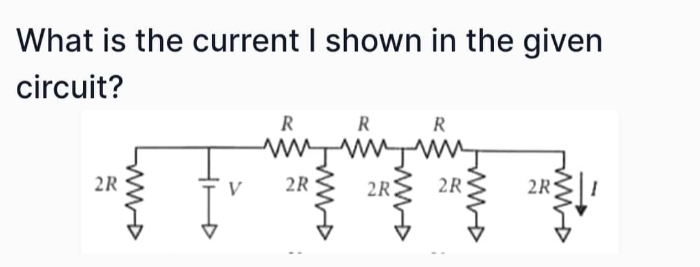
JEE Main - Physics
Asked by arivaryakashyap | 23 Apr, 2024, 10:40: AM
CBSE XI Science - Chemistry
Asked by rhythmdraco42 | 22 Apr, 2024, 10:43: PM
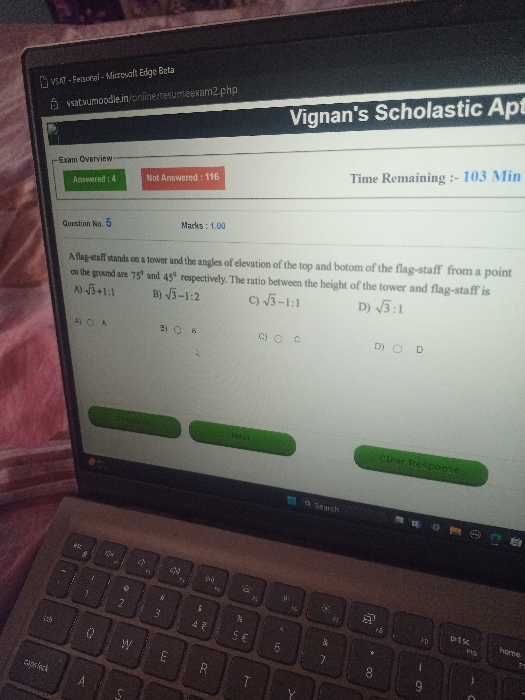
CBSE VIII - Maths
Asked by pinkiyadav79919 | 22 Apr, 2024, 08:03: PM
CBSE XII Commerce - Maths
Asked by hajarathvalishaik143 | 22 Apr, 2024, 11:32: AM