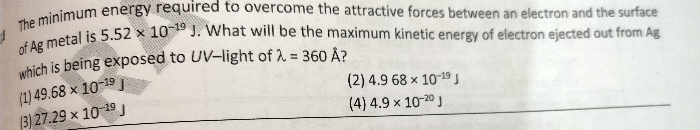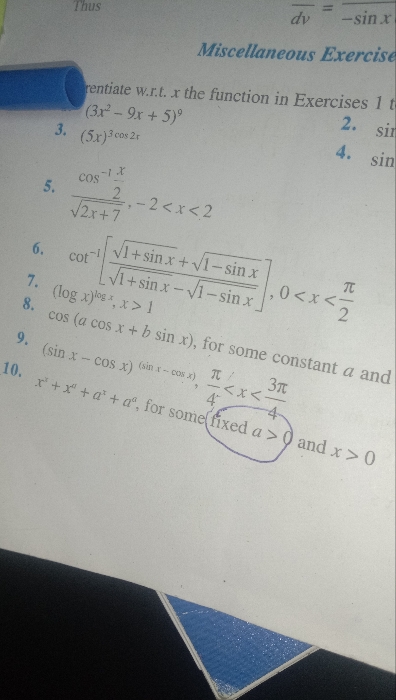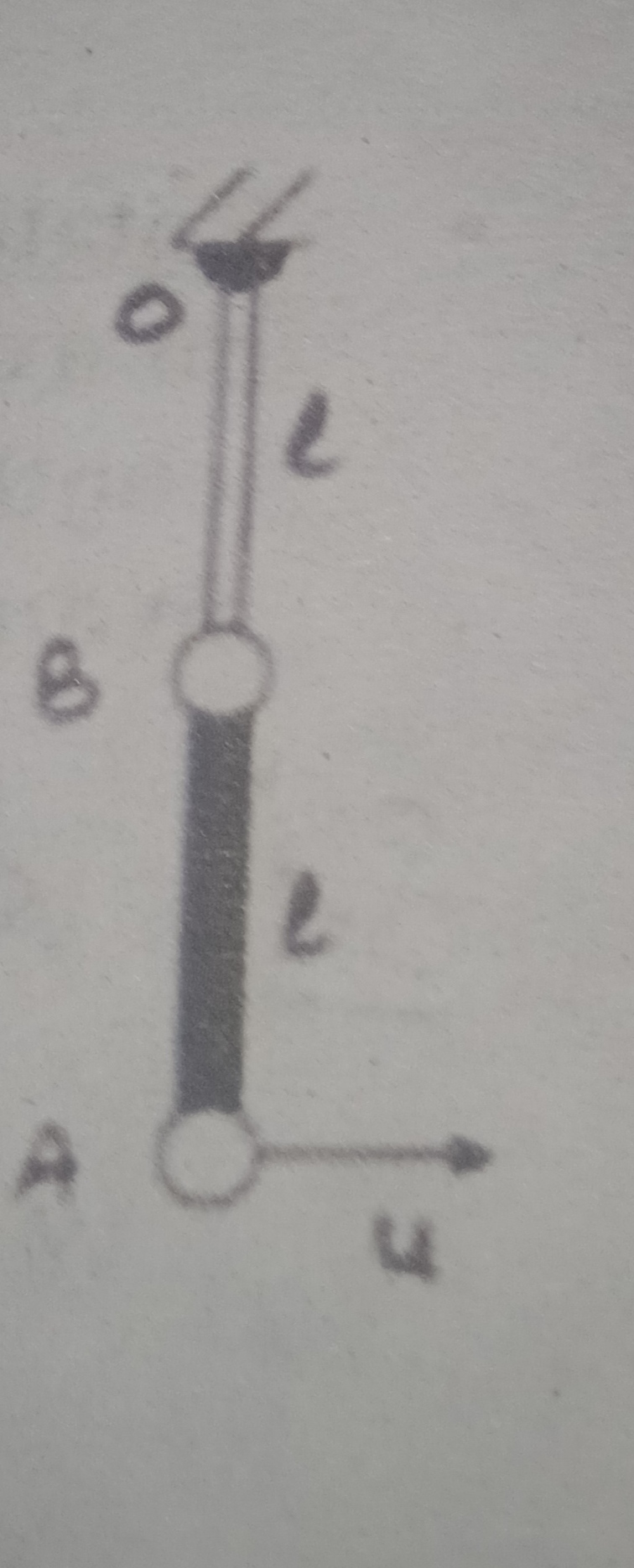Doubts and Solutions
OR
CBSE XI Science - Chemistry
Asked by saranyachakraborty2007 | 25 Apr, 2024, 05:23: AM
CBSE XII Science - Maths
Asked by aishaazmata | 24 Apr, 2024, 08:48: PM
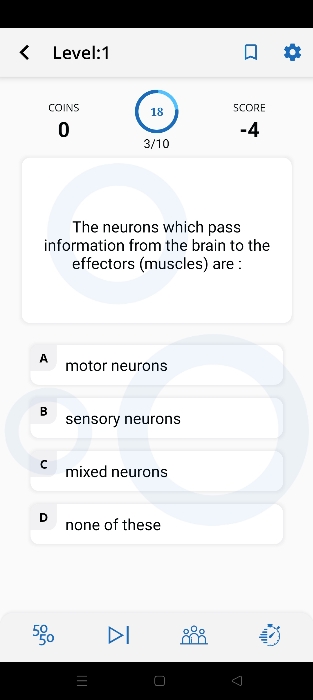
ICSE VIII - History and Civics
Asked by khatunrafika276 | 24 Apr, 2024, 06:57: PM
CBSE XII Science - Maths
Asked by revengesena | 24 Apr, 2024, 06:08: PM
CBSE VII - Maths
Asked by asthaenterprises2021 | 24 Apr, 2024, 04:58: PM
ICSE X - Maths
Asked by bhagvantingre | 24 Apr, 2024, 03:05: PM
CBSE XII Science - Physics
Asked by artabandhusahu85 | 24 Apr, 2024, 12:07: PM